数据结构与算法——回溯算法

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。

在代码中，我们通常使用递归函数来实现回溯算法，所以可以通过递归函数来了解回溯算法的机制。下面通过经典案例《八皇后问题》来学习了解这一算法。

八皇后问题

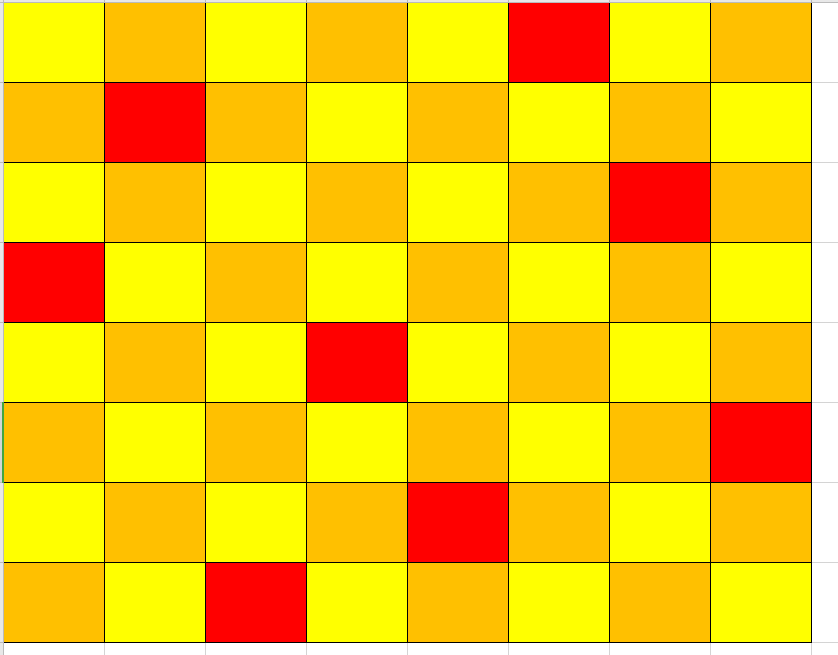
问题表述为：在8×8格的国际象棋上摆放8个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。

下图表示的是八皇后问题的其中一种解法，红色代表棋子位置，他们中每两个棋子既不在同一行，也不再同一列，还不在同一斜线。

回溯算法解决八皇后问题

通过回溯算法解决八皇后时，如果我们定义每个棋子的行为row；列为col；然后任意确认其中两个棋子分别为i,n。需要了解以下几点：

1. 判断同一行的公式为 row(i)==row(n)
2. 判断同一列的公式为 col(i)==col(n)
3. 判断处于一个斜线上的公式为 abs(row(i)-row(n))==abs(col(i)-col(n))

示例代码

• 封装类

package Queen8;

import java.util.ArrayList;

/**
 * 通过回溯算法解决八皇后问题
 */
public class Queen8 {
    /**
     * 棋盘大小
     */
    private int max = 8;
    /**
     * 存储棋子位置，其中index代表行，index对应的值代表列
     */
    private int[] way = new int[max];
    /**
     * 用于存储所有摆法的结果
     */
    private ArrayList<int[]> result = new ArrayList();

    /**
     * 开始计算
     */
    public void run(int n)
    {
        //当在第9此执行时，说明已经执行了8次，代表前8个棋子符合条件
        if (n >= 8) {
            this.result.add(this.way);
            this.print();
            return;
        }

        for (int i = 0; i < this.max; i++) {
            this.way[n] = i;
            if (check(n)) {
                this.run(n+1);
            }
        }
    }

    public void run()
    {
        this.run(0);
    }

    /**
     * 校验是否符合要求
     *
     * @return boolean
     */
    private boolean check(int n)
    {
        for (int i = 0; i < n; i++) {
            if (this.way[i] == this.way[n]) {
                //代表处于同一条直线上
                return false;
            }
            if (n - i == Math.abs(this.way[n] - this.way[i])) {
                //代表处于同一条斜线上
                return false;
            }
        }
        return true;
    }

    public ArrayList<int[]> getResult()
    {
        return result;
    }

    /**
     * 打印每一种方案
     */
    private void print()
    {
        for (int position : this.way) {
            System.out.print(position + " ");
        }
        System.out.println();
    }
}

• 代码执行

import Queen8.Queen8;

public class Main {
    public static void main(String[] args)
    {
        Queen8 queen8 = new Queen8();

        queen8.run();

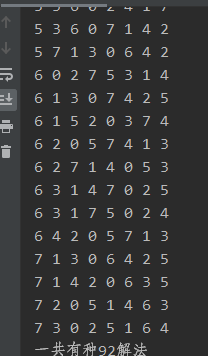
        System.out.printf("一共有种%d解法\t", queen8.getResult().size());

    }
}

• 结果展示