数据结构与算法——快速排序

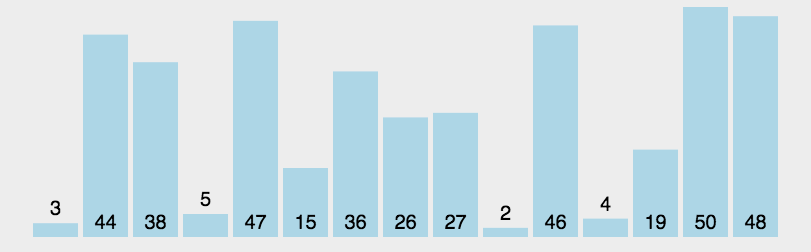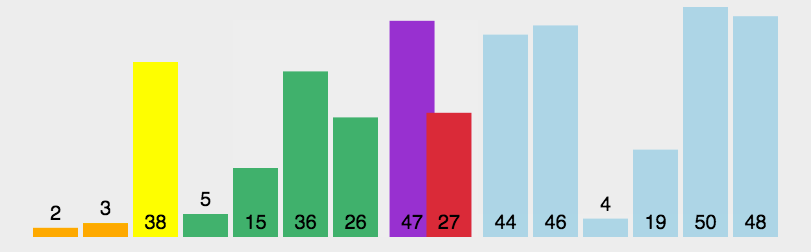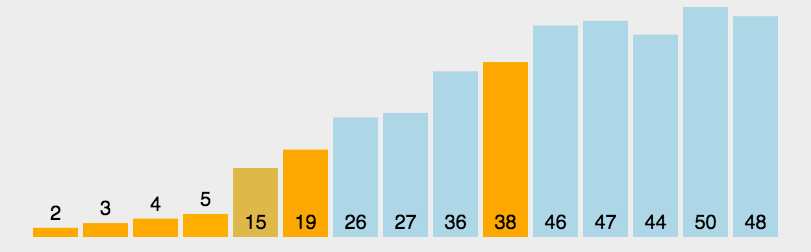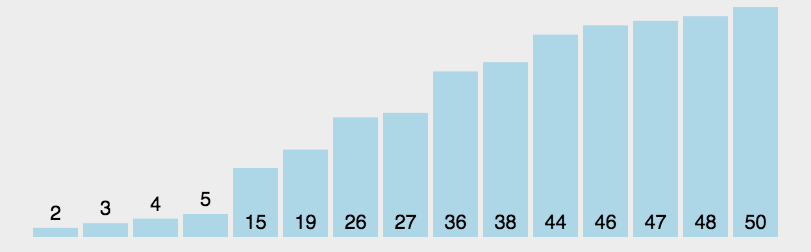
通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

算法要点

1. 在一个序列中，随机先找出一个基准点（基准点取得好不好，影响到快排的性能，后面回对基准点如何找进行详细学习并记录）
2. 将比基准点小的元素放在基准点的左侧，比基准点大的放在基准点的右侧
   • 从左到右依次与基准点比较，找到大于基准点的一个节点，并记录节点下标left
   • 从右到左依次与基准点比较，找到小于基准点的一个节点，并记录节点下标right
   • 如果left小于right，则交换两个节点
   • 重复以上步骤，直到right>=left
3. 对左右两侧的序列递归进行上述操作

基准点的选取

看了很多资料，目前大体选取基准点有以下几种方案

• 选取最左侧的节点
• 选取最右侧的节点
• 选取中间的节点
• 随机选取节点

其中，上述的方案各有优劣，在1,2方案中，基准点的选取更加方便，快捷，但是如果序列是一个已经排序好的，或者正好逆序的，那么这两种方案其实是最耗时的方案。3,4方案虽然会避免这种情况，但3方案会带着耗时的不确定性，4方案会增加随机算法的逻辑。为了中和这些问题，可以通过以下方案进行解决：

选取最左侧节点，选取最右侧节点，选取一个中间的节点，然后取出三个节点中中间元素作为基准值

动图演示

代码示例

package Sort;

import java.util.Arrays;

public class Sort {
    /**
     * 快速排序
     *
     * @param data  int[] 数据
     * @param left  int 左节点
     * @param right int 右节点
     *
     * @return int[]
     */
    public int[] quickSort(int[] data, int left, int right)
    {
        //记录一下原始的左右节点
        int l = left;
        int r = right;

        //选取一个基准点，为了方便，选取最后一个
        int pivot = data[l];

        while (l < r) {

            //找到左侧比基准点大的
            while (data[l] < pivot && l < r) {
                l++;
            }
            //找到右侧比基准点小的
            while (data[r] > pivot && l < r) {
                r--;
            }

            //交换两个值
            if (r > l) {
                int temp = data[l];
                data[l] = data[r];
                data[r] = temp;

                //这里需要注意一下，如果l节点与r节点相同并且等于pivot时候，也只会r--，
                // 所以即使存在重复的值，重复的值还是在第一个l的右侧，
                if (pivot == data[l]) {
                    r--;
                }

                if (pivot == data[r]) {
                    l++;
                }
            }
        }

        //左侧递归排序
        if (l < right) {
            data = this.quickSort(data, l + 1, right);
        }
        //右侧递归排序
        if (r > left) {
            data = this.quickSort(data, left, r - 1);
        }

        return data;
    }
}