数据结构与算法——计数排序

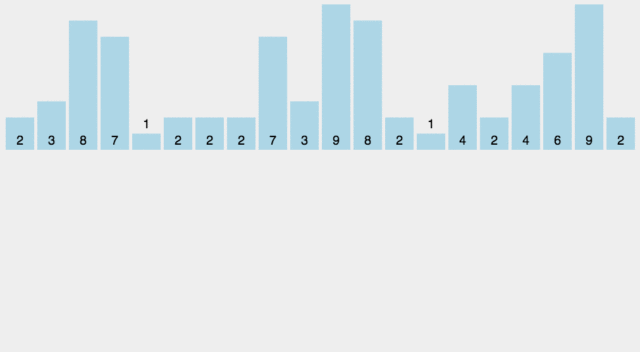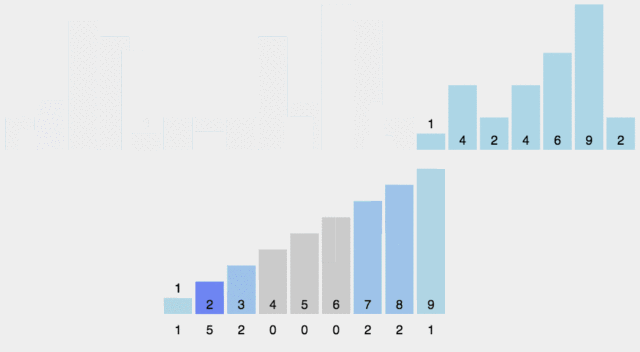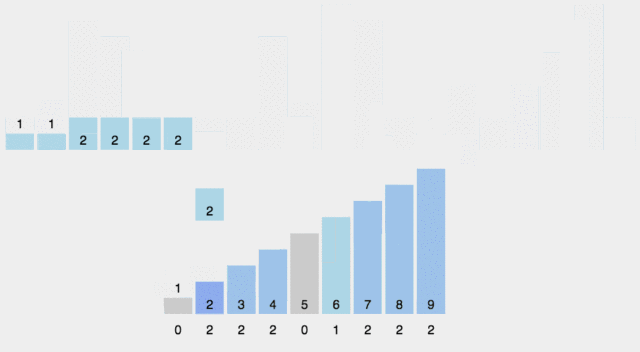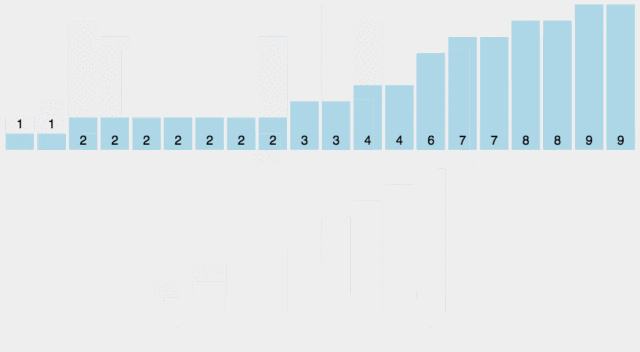
计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。

算法要点

1. 计数排序也是桶排序的一种，
2. 计数排序适用于数据量很大，但值分布范围很小的场景下
3. 第一步需要获取到序列中的最大值，最小值，创建一个长度为最大值-最小值的空的计数序列，其中序列的第0号4. 元素代表最小值的个数，以此类推
4. 遍历原始序列，根据每个元素的值，将对应计数序列中的值++
5. 遍历计数序列，根据计数序列中的每个元素的值，将原始序列依次填充。

动画演示

代码演示

package Sort;

public class Sort {
    /**
     * 计数排序
     *
     * @param data int[] 数据
     *
     * @return int[]
     */
    public int[] countSort(int[] data)
    {
        int max = data[0];
        int min = data[0];
        for (int i = 0; i < data.length; i++) {
            if (data[i] > max) {
                max = data[i];
            }
            if (data[i] < min) {
                min = data[i];
            }
        }

        int[] counterData = new int[max - min + 1];
        for (int i = 0; i < data.length; i++) {
            counterData[data[i] - min]++;
        }

        int index = 0;
        for (int i = 0; i < counterData.length; i++) {
            while (counterData[i] > 0) {
                data[index] = min + i;
                index++;
                counterData[i]--;
            }
        }

        return data;
    }
}