数据结构与算法——排序算法总结
时间复杂度
时间复杂度是判断一个算法的执行时间的性能指标,通常是一个代表算法输入值的字符串长度的函数,使用大O符号进行标数,不包括这个函数的低阶项和首项系数。
每一个算法都会存在一个实际的执行次数函数T(n),其中n代表的是每一个“操作单元”,并且认定每一个操作单元的所运行的时间都是相同的。如果将实际的执行次数函数T(n)中的低阶项、首项系数进行省略,就得到了我们所说的时间复杂度函数。省略的目标存在以下几点:
常数项省略
在一个算法中,如果T(n) = 2n + 3 + 1,那么其时间复杂度的影响受到n的影响要远远大于其中的3和1的影响,所以可以省略为T(n) = 2n
低阶项省略
在一个算法中,如果T(n) = n^2 + 2n + 3 + 1,可以省略其他的低阶项,记为T(n) = n^2
高阶项系数省略
在一个算法中,如果T(n) = 3 * n^2 + 2n + 3 + 1,可以省略其他的低阶项,记为T(n) = n^2
通过以上的各种省略机制,通常就可以得到时间复杂度的公式。需要注意的是,如果一个算法的执行次数函数为T(n) = 3 + 1,那么通常认为这个算法的事件复杂度为常数阶(O(1))
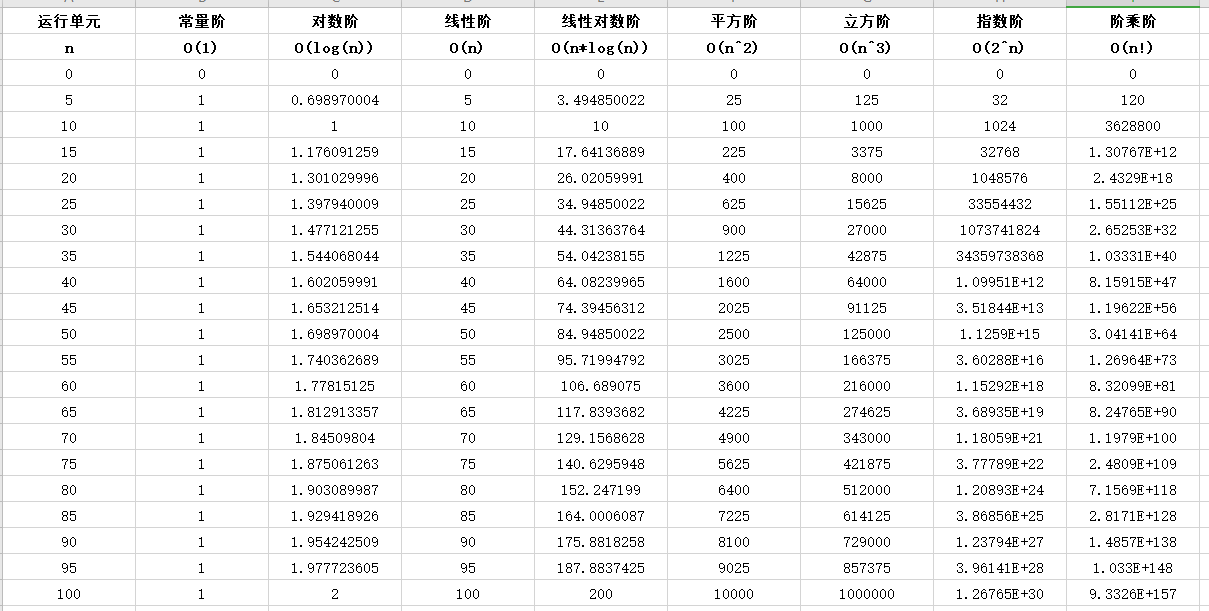
常见时间复杂度种类
- 常量阶 O(1)
- 对数阶
- 线性阶
- 线性对数阶
- 平方阶
- 立方阶
- 指数阶
- 阶乘阶
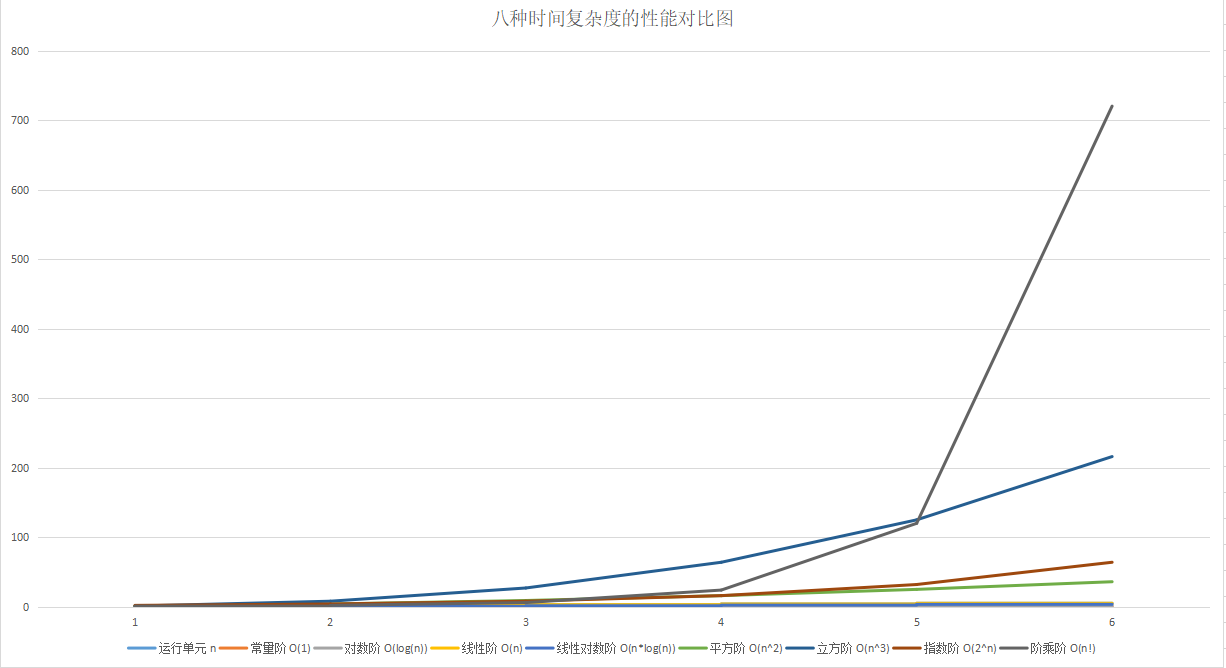
下面将这八种时间复杂度的制作为一张数据图标,以方便展示其性能的优劣
空间复杂度
空间复杂度的内容类似于时间复杂度,其是用来衡量一个算法的所占用内存的性能指标,其中的n代表的是每一个“占用空间”,并且认定每一个占用空间都是相同的。
为什么不需要关注空间复杂度
- 目前大多数的算法本质上就是空间换时间
- 硬件发展的越来越迅速,内存的成本较低
常见的排序算法
根据排序方式,可以将排序算法分为两大类:内部排序和外部排序
- 内部排序:整个排序过程不需要访问外存便能完成
- 外部排序:整个排序过程不可能在内存中完成
常见的排序算法
- 冒泡排序
- 选择排序(简单选择排序)
- 插入排序
- 快速排序
- 希尔排序(shell排序)
- 堆排序
- 归并排序
- 计数排序
- 桶排序
- 基数排序
排序算法
总结
快速记忆法:“选泡插”,“快归希”,“计基桶”
- 基础排序算法为三个:选(选择排序)泡(冒泡排序)插(插入排序)
- 希尔排序,又名“缩小增量排序”,是插入排序的优化,通过不断的缩小步长、增加组数,实现跨越多个数的进行 插入排序,实现其优化
- 快速排序,是冒泡排序的优化,通过递归模式,将基准点的左侧设为比其小的元素,右侧设为比其大的元素,实现冒泡优化
- 归并排序,通过递归拆分,然后通过递归合并进行排序
- 基数排序,属于“桶排序”的一种,依次根据每个元素的不同位数的值插入到桶中,然后在取出,知道排序完成。
- 计数排序,属于“桶排序”的一种,先计数,然后在根据计数生成或插入到原来的序列中,完成排序
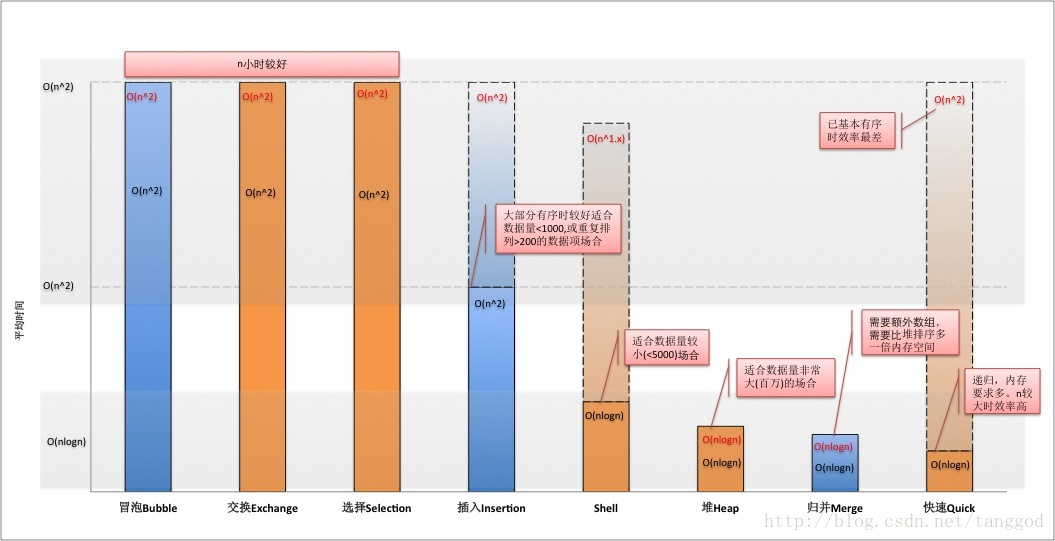
排序算法对比
| 排序法 | 平均时间复杂度 | 最好情形 | 最差情形 | 空间复杂度 | 排序方式 | 稳定度 | 备注 |
|---|---|---|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | In-place | 稳定 | n小时较好 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | In-place | 稳定 | n小时较好 |
| 插入排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | In-place | 稳定 | |
| 希尔排序 | O(n log n) | O(n log2 n) | O(n log2 n) | O(1) | In-place | 不稳定 | |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) | Out-place | 稳定 | n大时较好 |
| 快速排序 | O(n log n) | O(n log n) | O(n^2) | O(log n) | In-place | 不稳定 | n大时较好 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(k) | Out-place | 稳定 | |
| 桶排序 O(n+k) | O(n+k) | O(n^2) | O(n+k) | Out-place | 稳定 | ||
| 基数排序 | O(n+k) | O(n+k) | O(n^2) | O(n+k) | Out-place | 稳定 |
- 稳定度:如果a原本在b前面,a=b,排序后a仍然在b前面,则代表稳定;如果不确定,则代表不稳定
- 排序方式:所有排序操作都在内存中完成,称为内排序;如果排序通过磁盘和内存的数据传输才能进行,称为外排序
- 时间复杂度
- 空间复杂度
- 参数表示含义
- n: 数据规模
- k: 桶的个数
- In-place: 不占用额外的内存空间
- Out-place: 占用额外的内存空间